Archive

Tag Archives: inequality

The Infinite Horizons of a Good Education

March 22, 2013
the Economy: Home and the World
2 Comments

Evan Soltas has a very interesting blog post about intergenerational inequality. The thrust of his argument is that inequality in educational attainment exists, even adjusting for differences in income. At some level, this is trivial – one would expect educated parents, wealthy or not, to spend more on academic pursuits for their children. The conclusion Evan draws, however, is quite fantastic that is, the effect of educating a kid today is geometrically valuable:

Here’s why that math is important. The high school dropout rate among people whose fathers were dropouts is 22.2 percent. The dropout rate with high-school-grad fathers is 2.9 percent. Let’s assume that the social value of a high school degree is $30,000 per graduate; that’s roughly the difference in average income between non-grads and grads. Public policy that supposes they are helping one person assesses the value of that degree at $30,000, obviously. Public policy that supposes they are helping an infinite succession of people assesses the value of that degree at $819,000.

He arrives at a whopping $819,000 as the difference in the net present value of fathers with and without high-school degrees in terms of the future earning potential of their kids. I would argue that the value of a high-school degree is somewhat less than $30,000 because a good amount of the delta is derived from the further division between college graduates and non-graduates. This wouldn’t change the situation if the deviation was randomly distributed (and college actually added value, a contestable claim), but there’s good reason to believe it’s not. (For example, there are definitely demographics in which it’s very likely a child graduates high school, but also very unlikely that he or she graduates a 4-year college).

That even basic jobs require a college degree nowadays would further diminish the value of a high school degree by itself. The $819,000 figure includes the increased chance of attending college, which is far more dubious in its actual value added. A more conservative, but not necessarily better, approach would be to estimate the value added by high school itself, assuming that college adds no value, or approximately $11,000, according to Pearson.

The geometric multiplier is about 26.15, yielding a present value of $298,615. This isn’t nearly as astonishing as Evan’s $819,000, and probably isn’t as close to the truth. However, it does compound an already compelling case for investing in high school education; that it’s worth it even if no one ends up at college. At a public school, the average cost per pupil is $10,652 or about $40,000 for a degree, or a 645% return on investment. This is a low-hanging fruit.

I think there’s one big flaw in the way Evan looks at things; it’s also important to note that the value of a high school education is hugely understated by the calculated figure, because it is the difference in annual income. The effect over a lifetime is many multiples of this. For this reason, the return on a high school degree, a net of 645%, doesn’t begin to approximate the real value of an education.

A final caveat, I have a pretty strong feeling that education by itself doesn’t explain the intergenerational inequality in education. As it happens, I came across this passage in a recent copy of the Economist:

The well-to-do [have] largely held to old-fashioned ideas about marriage. Among professionals, births within marriage are four times as common as births where the father is registered as absent from the household.

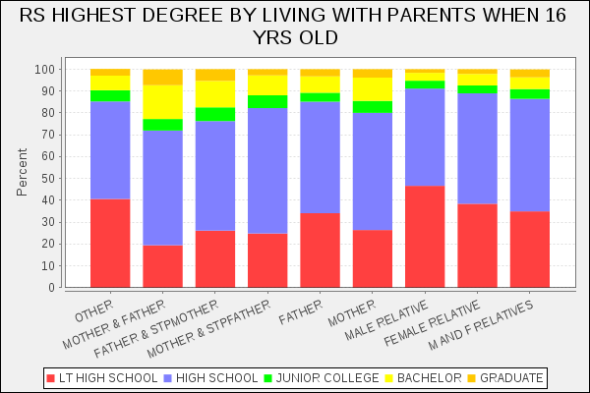
This is for Britain, but the gap is only worse in America. The figure below charts educational attainment of a child by family situation at age sixteen.

Image

One can see an almost twofold increase in dropout rate between dual and single guardian households (the exception being families where neither of the guardian is directly related to the child). The geometric multiplier between a nuclear family and anything but is about 20. While this is less than that of a high school degree, the policy cost is also substantially less than $40,000.

Today, in many ways, we disincentivize marriage – as Nicholas Kristoff grimly notes – with poorly designed welfare programs (such as handouts to single mothers). As the Economist notes, I don’t believe the chain of causality is as strong between an educated parent inculcating similar values in his children as much as strong tendencies towards the nuclear family among the educated, which themselves engender stronger attitudes about education.

Regardless, any of these points are a damning indictment of the “American dream”. Policymakers need to acknowledge the importance of a high school education. We’ve spent billions in grants and subsidized student loans for college that implicitly benefit the lucky, that is those who already have a high-school education.

Further, it is far from established that college today adds economic value to society. The huge underemployment of recent graduates (which itself causes the unemployment of those without a college degree) should make each of us think twice while promoting the virtues of college.

Indeed, the advent of online courses further convinces me that college is but a licensing factory. For example, a University of Washington course in Financial Econometrics is provided on the Coursera platform, with the additional option of doing slightly more work and receiving slightly more attention, at a price tag of $4,000. This is absurd. The only value derived from the for-credit option is Washington’s official stamp of approval, a license.

By blindly subsidizing college education we’re implicitly encouraging rent-seeking behaviors that are damaging to society as a whole, especially those at the bottom. Evan’s point is clear: we need to stop acting like a high school degree is its present value, so long as inequality persists. Indeed, Evan hugely underestimates the value of his own claim by ignoring the lifetime effect of increased cash flow. For those of you interested in that figure, even discounting at 15%, it’s over $10 million.

The poor can save too: Here’s how we can help

March 12, 2013
the Economy: Home and the World
2 Comments

Noah Smith has an article in The Atlantic about wealth inequality in the United States. A viral video caught the attention of the economics-blogosphere, and Noah is the latest to comment.  The import of Noah’s argument is the importance of thrift:

Today, wealth equality is closely tied to income equality. But in the long run, it’s all about thrift, frugality, and saving — in other words, teaching a consumer nation a lesson in cheapness.

Progressives have a hard time ascribing wealth inequality to savings rate and (predictably, though not incorrectly) blame structural issues like falling wage share of income. As one very popular commentator notes:

This is absurd. The real wealth gap is based in capital gains, not direct income. Teaching Americans to be frugal is not going to address any of the systemic differences that make it easier by orders of magnitude for the already rich to keep making money.

The fact is, poor American’s can save, they just have really bad habits. For example, as Derek Thompson notes, the poor spend a whopping 9% of their income on lottery tickets. So let’s be honest here, the whole diatribe against Noah that the poor can’t save is crap.

If we’re going to talk about wealth inequality, it’s pretty informative to understand its emergence, why it’s fundamentally different from income inequality, and why an “equal” society won’t help. Consider, an island which is functionally equal – you might say socialist. I’m not suggesting this is a plausibly sustainable situation, but it’s an interesting starting point. Let’s also assume that somehow socialism hasn’t eroded work ethic and desire to innovate. In reality, this isn’t a reasonable assumption, but I’m not making an argument about economic ideology.

So, on day one, the Keynesian economist, farmer, laborer, and lawyer each earn $100 a year. The economist is a spendthrift, with a good taste for Portuguese wine and Victorian clothes, and has only $10 left each year. The laborer, saves diligently, and has $50 leftover. Very soon, an island that once had income equality becomes very unequal, both in income and wealth. The wealth inequality comes first, but soon the laborer has more money to invest in his daughter’s education, and to loan to the moderately-thrifty lawyer and farmer to earn a good return.

So wealth inequality comes first. This is especially true if you consider, in our society, income derived from education to be a capital gain (though, legally, it is treated as labor). In the island, wealth and income inequality were both functions of preference.

However, in our society, as wealth inequality isn’t just a function of preferences, but income itself (in the island this isn’t the case because future income inequality is derived from wealth inequality which itself is derived from preferences). But, in a given snapshot, wealth inequality grows as, in some ways, the integral, roughly speaking, of income inequality.

This is because, if preferences are randomly distributed, the savings become a function of income. As income inequality rises (as it has in the past 40 years), the ability to save gets rather more concentrated amongst the rich. This, and not preferences, becomes the key force of wealth inequality. This is further compounded by the fact that, in a very literal sense, wealth begets wealth through capital income.

So my point of all this is I think Noah’s wrong that somehow altering preferences will fix the situation. Noah argues that, for a “return to equality”, the poor need to be nudged and educated:

In addition to “nudging” middle-class and poor Americans to save more, we can help them get a better return on their assets — the second thing that has a huge effect on wealth in the long run. This means helping middle-class people invest in stocks without paying high fees. The first part of this is teaching middle-class people to avoid making frequent changes in their stock portfolios. Studies show that individual investors consistently lose money when they try to buy and sell and buy and sell, mostly because they tend to ignore trading costs. So financial education should teach people to let their stock portfolios just sit there for decades, and ignore the ups and downs.

The second way to get better returns is to avoid actively managed funds. Actively managed mutual funds charge high fees to purchase portfolios of stocks that, statistically, are no better than simply buying a low-cost “index” fund that tracks the overall level of the market. Pension plans like TIAA-CREF tend to charge even higher fees, meaning even worse returns. Financial education can teach middle-class people what a low-cost index fund is, and how to invest in one.

The first point is rather interesting, and Richard Thaler has the best evidence that it might work (Save More Tomorrow – fantastic study, I think everyone should read it). I don’t have much to say about personal finance education, I think it’s important, but I just don’t think it will have a lasting effect on habits in a consumer culture. Education will be artificial and instituted in the context of grades, which will be the only reason people pursue the subject.

But, as I argued, changing preferences will have only an ephemeral effect. What we need are:

  • Robust risk sharing programs (particularly universal healthcare, strong social insurance, and unemployment insurance). This will a) decrease the need for wealth, mitigating the effect of wealth inequality and b) allow the poor to invest most of their income in stocks, so that they can take part in America’s wonderful capital market. Noah mentions China a country that’s poor but manages to save a lot. One of the many reasons for this, I believe, is an underdeveloped insurance market, creating a greater need for wealth.
  • Ban lotteries. This is simple. Sure, states make a lot of money from them, but this is absolutely the most regressive tax in the country. Not only are educated people informed enough to know that the state has an edge, but it’s a very small part of their income.
  • “Nudge” Americans to save through opt-out programs sponsored by an employer.
  • Institute a progressive consumption tax with negative income
  • Fix income inequality.

The integral-relation with income inequality explains why it will always grow as income inequality is constant, but wealth distribution doesn’t need to be as skewed as it is. Preferences will go some way, but the real change needs to come from income distribution (by investing in human capital) and access to capital markets (by pooling risk).

The falling role of labor in our economy will make wealth very important. Acting now is a pretty good idea. But, moving on, let’s remember a few things: demand creates supply, and wealth inequality creates income inequality. Let’s not mistake cause and symptom.

Normative questions belong to economists too

March 6, 2013
the Economy: Home and the World
2 Comments

@DavidA on Twitter points us to an old post by Joe Seydl arguing that economists are no longer allowed to speak about normative social problems, like inequality or climate change:

I propose a new rule: economists are no longer allowed to speak about normative social problems, such as rising inequality or climate change. Let’s leave the discussion of such problems to the philosophers.

The justification for this rule comes from the fact that solutions to normative social problems require selfless thinking. And there is ample evidence to suggest that economists behave in more self-interested ways than do noneconomists.[1]

Consider rising inequality. The philosophical justification for rising inequality can be found in John Rawls’ philosophy. In “A Theory of Justice,” Rawls argues that it is just to increase inequality up to the point where any further increase would leave the position of the least-well-off member of society unchanged. In other words, any increase in inequality that is worth bearing, according to Rawls, must benefit the worst-off members of society in some discernible way. This is known as Rawls’ Difference Principle.

A starting point for Rawls’ Difference Principle, however, requires that one at least has concern for the least-well-off members of society. Economists clearly don’t meet this criterion, because the distribution of efficiency gains rarely matters to them; why else would the majority of economists support a whole host of free-trade agreements that put manufacturing workers in direction competition with workers overseas, while at the same time protecting highly paid professionals, such as doctors and lawyers, from the same competition? The answer, of course, is that economists do not care about the well-being of manufacturing workers.

[…] Or consider climate change. It is all well and good if resources are allocated in such a way that leads to high productivity growth and rising living standards in the near term, but what about the longer term? Efficiency gains are “worth it,” according to the philosophers, if the gains are sustainable; and, importantly, if the gains are sustainable over many generations. If rising living standards over the next few decades come at the expense of more frequent droughts, floods, and devastating heat waves for future generations, then the near-term gains are probably not be worth pursuing.

Economists are incapable of thinking about sustainable development, because sustainable development requires a concern for the well-being of future generations. The rational-choice model that dominates neoclassical economics assumes that individuals are always in pursuit of their own material self-interests, saying nothing about the interests of future generations.

The rational-choice model may or may not be an accurate description of human behavior; there is evidence to suggest that humans often act irrationally, especially when it comes to their evaluation of sunk costs or charitable givings.[2] But it doesn’t matter, because so long as exposure to the rational-choice model increases the likelihood of selfish behavior, the implication is that economists will be in an increasingly poor position to evaluate normative social problems.

Economics wasn’t always this way. For example, in the 1940s, 1950s, and 1960s, Paul Samuelson wrote a great deal about the mixed-economy model, which stressed the importance of development on three fronts: efficiency, fairness, and sustainability.[3] (The latter two requiring selfless thinking.) But it’s unlikely that the profession will ever adopt a more outward stance on human behavior, as the standard rational-choice model can be thought of as a relentless force that only grows stronger with time.

For this reason, it makes sense to limit what economists are allowed to speak about, rather than sit around wondering whether economists will one day incorporate selflessness into their behavior models. If economists would like to speak about profit maximization in a particular market or how economies of scale differ across markets, then fine. But, please, let’s leave the normative questions to the philosophers.

Anyone who’s fully content with the way modern economics works needs to wake up. Even pretty ardent supporters of the EMH (like Larry Summers or Alan Greenspan) accept this. The recent financial crisis gives full life to this concern. However, the concern voiced in this quote is misguided in theory, and can be dangerous in practice.

Consider the Rawls’ Difference Principle. Without economic reasoning and analysis, how exactly is one supposed to figure out “the point where any further increase [in inequality] would leave the position of the least-well-off member of society unchanged” ? More importantly, what way to philosophers have to determine the “right” philosophy (at least economists are getting to the point where their convictions are either justified or falsified by data).

A radical philosopher (I’m thinking his name starts with an ‘M’ and ends with an ‘X’) might suggest that any level of concentrated capital ownership breaches this principle. In ideality, we would have an equally poor society, and in reality we would get Josef Stalin. Full disclosure, I think Marx was a terrible economist, but a pretty fantastic sociologist, ahead of his time.

This post also ignores that there are plenty of philosophers who are okay with an entirely self-interested society. Conversely, many economists are in favor of a kind and caring society. Indeed, the father of classical economics, Adam Smith, was himself believed that charity and trust ought to underpin any capitalistic society. Note the normative claim.

On the other hand, we have philosophers like Ayn Rand who believed love and marriage were for idiots, and atheistic selfishness was the way of the future.

The idea that economists can’t handle climate change is equally dubious. Indeed, I think global warming can be solved, entirely, in the hands of modified neoclassical thinking. The problem with simple economic models is the consideration of oil, gas, and coal as cash flow rather than capital stock while treating a sustainable environment as a public good rather than eroding resource. This is an idea embraced by E.F. Schumacher in Small is Beautiful. Though, unlike me, he prefers a Gandhian-agrarian society to capitalism. It was also this idea that compelled one of history’s most brilliant men, Buckminster Fuller, to suggest that the natural cost of oil is over a million dollars per barrel.

Within neoclassical models, were these assumptions of measure to be changed, we would very quickly move towards rapid carbon taxation and renewable energy. Further, it requires science and calculation to solve this problem, not the normative whims of an armchair philosopher. Indeed, it is the social philosopher within the economist that averts a wider cry for high carbon taxes.

Even conservative mainstream of economists, like Professor Mankiw, believe in an economic solution to our environmental problem. However, it is the the knowledge that a rapid decarbonization will corrode our society and political institutions that prevents a move towards this tax. 

If we’re going to talk about mistakes economists have made why not John Locke’s idiotic defense of slavery. Indeed, it’s quite a bit easier to contrive philosophy towards a defense of slavery than it is any form of economics, which would argue that the abridgment of individual agency in commerce would broke a society. An economist’s argument; but a right argument.

The rational-choice model is widely criticized, at least in its simplistic form, even within the economics community. Not because it doesn’t yield the fair outcome, but because in our modern society it makes inane assumptions (no, I don’t consider my potential income in the year 2050 and raising interest rates against my utility function for a given tomato in making my purchase). That doesn’t mean the economics mindset is wrong, it means it has to change.

This post further assumes all economists would fall under the narrow realm of ‘mainstream’ economists. Plenty, have argued for a more equal society. What makes a philosopher more suited to judge “what is just”. Or, a more potent question, what makes a philosopher?